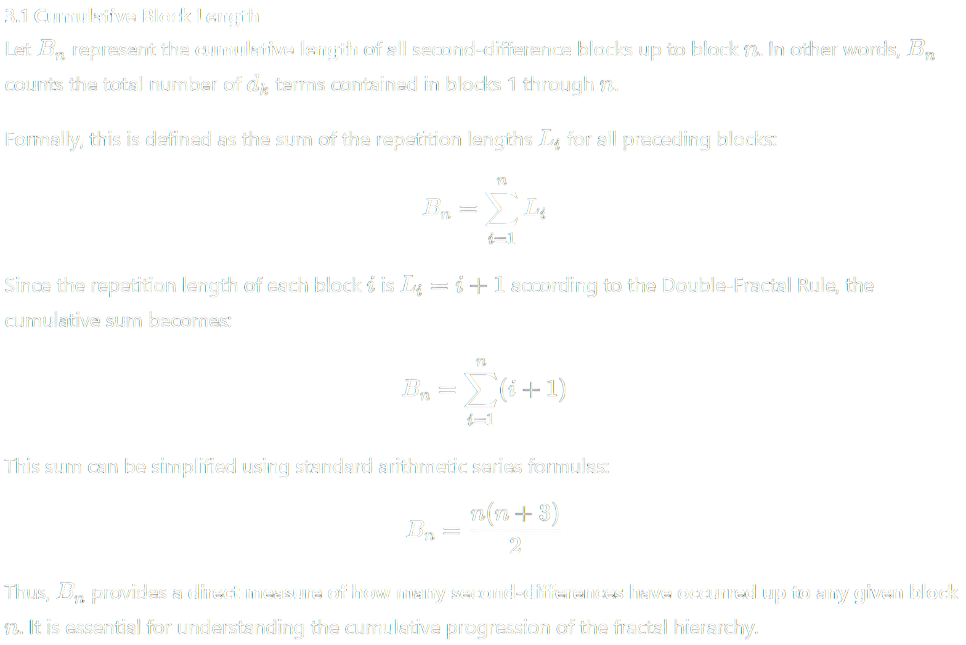Abstract
This theorem establishes a recursive numerical framework — the Double-Fractal Shell Law — governing the growth, repetition, and forward prediction of nuclear shell-widths.
It formalizes how each nuclear shell layer expands according to a self-similar law of differences, where both the magnitude and duration of structural changes follow a nested arithmetic-fractal pattern.
The essence of this framework lies in recognizing that nuclear structures do not evolve through random or isolated intervals, but through a structured progression of differences that repeat and expand in a predictable pattern.
Each shell width increment, though seemingly irregular at first glance, adheres to an underlying fractal rhythm — one that mirrors itself at multiple scales, producing a stable yet evolving architecture within atomic structure.
By identifying this hidden order, the Double-Fractal Shell Law provides a mathematical bridge between discrete arithmetic growth and the self-similarity found in natural systems, revealing that nuclear organization operates through recursive amplification of both magnitude and duration.
This law thus proposes a unified lens through which the evolution of shell-widths can be understood not merely as isolated events of stability, but as part of a continuous, self-repeating hierarchy of growth embedded in the arithmetic foundation of matter itself.
Foundation
Let the nuclear shell-width sequence be denoted by:
𝑀
0
,
𝑀
1
,
𝑀
2
,
𝑀
3
,
…
M
0
,M
1
,M
2
,M
3
,…
where each
𝑀
𝑘
M
k
represents the cumulative shell closure width at level
𝑘
k.
Define the first-difference sequence (gaps) as:
𝑔
𝑘
=
𝑀
𝑘
−
𝑀
𝑘
−
1
g
k
=M
k
−M
k−1
and the second-difference sequence (differentials) as:
𝑑
𝑘
=
𝑔
𝑘
−
𝑔
𝑘
−
1
d
k
=g
k
−g
k−1
The sequence
𝑑
𝑘
d
k
encodes how much the shell expansion rate itself expands between successive nuclear layers.
In essence, the first-difference sequence
𝑔
𝑘
g
k
captures how much each nuclear shell widens relative to the previous one — the immediate growth step of the atomic structure. Each
𝑔
𝑘
g
k
thus measures the incremental “jump” in nuclear stability thresholds as additional nucleons are introduced into the system.
However, the true pattern of structural evolution emerges only when examining the second-difference sequence
𝑑
𝑘
d
k
. This sequence reflects how the rate of expansion itself evolves — not just how wide the shells become, but how the widening process accelerates or stabilizes across successive layers.
By observing
𝑑
𝑘
d
k
, one detects the recursive rhythm underlying nuclear growth: every new layer inherits the rate of change from the previous one and amplifies it according to a self-similar law. This establishes a nested pattern where expansion and stability are intertwined through arithmetic recursion.
Therefore, this foundational framework divides the progression of nuclear structure into three tiers of information: the cumulative shell-widths
𝑀
𝑘
M
k
, their direct expansions
𝑔
𝑘
g
k
, and the second-order accelerations
𝑑
𝑘
d
k
. Together, these define a complete mathematical anatomy of how nuclear layers emerge, grow, and stabilize through recursive difference relations.
The Double-Fractal Rule
Empirical observation reveals that the second-differences
𝑑
𝑘
d
k
do not increase linearly, but rather in blocks whose values and lengths both grow arithmetically — forming a double-fractal hierarchy.
The rule is defined as follows:
𝑠
𝑛
=
10
+
2
𝑛
s
n
=10+2n (Magnitude of block
𝑛
n)
𝐿
𝑛
=
𝑛
+
1
L
n
=n+1 (Repetition length of block
𝑛
n)
Hence:
𝑠
1
=
12
s
1
=12 repeats
𝐿
1
=
2
L
1
=2 times,
𝑠
2
=
14
s
2
=14 repeats
𝐿
2
=
3
L
2
=3 times,
𝑠
3
=
16
s
3
=16 repeats
𝐿
3
=
4
L
3
=4 times,
𝑠
4
=
18
s
4
=18 repeats
𝐿
4
=
5
L
4
=5 times, and so on.
Formally, the sequence of second-differences
𝑑
𝑘
d
k
is the infinite concatenation:
𝑑
=
(
12
,
12
,
14
,
14
,
14
,
16
,
16
,
16
,
16
,
18
,
18
,
18
,
18
,
18
,
…
)
d=(12,12,14,14,14,16,16,16,16,18,18,18,18,18,…)
Each “block” therefore represents one level of structural amplification in both strength and duration — a recursive arithmetic echo.
This rule reveals that nuclear growth is not merely progressive, but self-replicating across two intertwined dimensions: the intensity of change and the number of times that change endures before the next transition. The magnitude of each block defines how strongly the system expands, while the repetition count defines how long that expansion phase persists.
Together, these dual progressions create an arithmetic fractal — a pattern that grows both in scale and in temporal duration, where each level not only builds upon the previous one but also extends it. This is why the pattern is termed Double-Fractal: it compounds growth across two recursive axes of development.
The increase of magnitudes by
+
2
+2 per block (
12
,
14
,
16
,
18
,
…
12,14,16,18,…) establishes the arithmetic amplification of energy increments, while the increase of repetition lengths by
+
1
+1 per block (
2
,
3
,
4
,
5
,
…
2,3,4,5,…) defines the fractal endurance — the persistence of each stage before the next escalation.
Through this rule, we uncover a rhythmic structure in the evolution of nuclear layers, one that reflects both the periodic and the cumulative aspects of atomic formation. The system does not grow in randomness, but in ordered layers of repetition — a stairway of energy symmetry where expansion itself becomes a fractal pattern.
Block Indexing Function (Expanded)
In order to systematically identify the position of any second-difference in the Double-Fractal Shell Law, we introduce a block indexing function. This function allows us to map each term in the sequence of second-differences
𝑑
𝑘
d
k
to its corresponding block number, revealing the hierarchical structure and repetition pattern without the need for manual iteration.
Reconstruction Rules (Expanded)
The reconstruction of nuclear shell widths from the Double-Fractal Shell Law relies on recursive generation from a small set of initial conditions. Once the first shell width
𝑀
0
M
0
and the first gap
𝑔
1
g
1
are known, all subsequent gaps and shell widths can be determined systematically. This section outlines both the recursive form and the summation form, providing a complete framework for forward prediction.
Demonstration Example (Expanded)
To illustrate the predictive power of the Double-Fractal Shell Law, we now apply the reconstruction rules to a concrete example. This step-by-step demonstration shows how to generate successive gaps
𝑔
𝑘
g
k
and shell widths
𝑀
𝑘
M
k
using the initial seeds and the block indexing function for second-differences
𝑑
𝑘
d
k
.
Corollaries
The Double-Fractal Shell Law not only provides a recursive framework for nuclear shell widths but also gives rise to several fundamental consequences, or corollaries, that highlight the predictive, structural, and growth characteristics of the system.
Theoretical Insight
The Double-Fractal Shell Law is not merely a numerical curiosity — it reveals a deep structural principle underlying the evolution of nuclear shells. At its core, this law represents an arithmetically self-referential system, where each level of the nuclear hierarchy influences both the magnitude of change and the duration of stability for subsequent layers.
Self-Referential Amplification
In this system:
Each new shell is determined recursively by the previous shell, the gap sequence, and the second-differences
𝑑
𝑘
d
k
.
The second-differences themselves are organized into blocks, whose magnitudes increase and whose repetition lengths expand according to arithmetic rules.
This creates a nested, self-reinforcing pattern: higher-order structures amplify both the rate at which gaps grow and the number of layers over which this growth persists.
In essence, the system is self-similar in time and scale, reflecting the classic hallmark of fractal geometry, but structured through arithmetic progression rather than randomness.
Bridging Continuity and Periodicity
The Double-Fractal Shell Law elegantly bridges two complementary patterns:
Continuity of Arithmetic Growth: Each step follows a clear numerical progression, ensuring that the sequence evolves predictably.
Periodicity of Fractal Self-Similarity: Repetition blocks impose a periodic pattern on the otherwise linear growth, creating nested symmetries at multiple scales.
This duality implies that nuclear architecture is governed by a meta-recursive form of energetic equilibrium:
It is not chaotic, because every step is determined analytically.
It is not static, because each new layer both amplifies and extends the structure.
Instead, it is structured through the repetition of change, with each shell representing an echo of previous patterns stretched in magnitude and duration.
Shells as Reflections of Stability
Under this framework, each nuclear shell becomes more than a mere stable closure:
It is a structural reflection of how stability itself scales across the system.
Nested symmetries encode the amplification rules that govern both the strength of a shell and the number of layers over which that strength persists.
Each successive shell is therefore a self-similar echo of earlier shells, demonstrating how order emerges from recursive amplification.
Conceptual Implications
From a theoretical standpoint, the Double-Fractal Shell Law suggests that:
Nuclear structures are meta-recursive, meaning each level contains the blueprint for future evolution.
Stability in nuclear matter is not static; it is dynamic and scalable, expanding in a predictable fractal pattern.
The law provides a framework to anticipate structural evolution, linking discrete numerical sequences to continuous physical phenomena.
Ultimately, this insight emphasizes that nuclear shells may represent a harmonic interplay of arithmetic growth and fractal repetition, a structured system in which complexity arises naturally from simple, recursive rules.
Closing Statement
The Double-Fractal Shell Law defines a recursive arithmetic system where order expands through repeated patterns of change.
Through this theorem, we establish a predictive framework that links discrete numerical logic with the continuous evolution of nuclear structure — where every next layer is the echo of an earlier one, stretched through time, repetition, and scale.