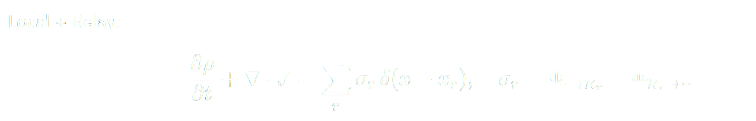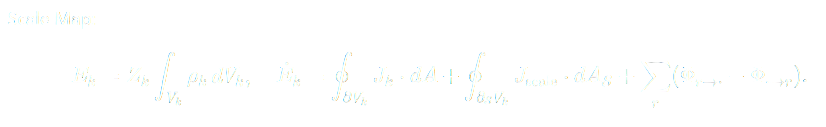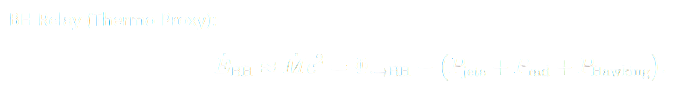TL;DR
If total energy is conserved locally while the universe’s geometry and “scale of description” both change, then what looks like creation or loss at one scale is a transfer across (i) space-time funnels (e.g., horizons) and (ii) descriptive scales (micro ↔ macro).
At the microscopic level, energy transformations may appear as particle creation or annihilation, yet these events are simply redistributions of energy within a closed local framework. As systems scale upward—from atoms to stars to galaxies—the curvature of space-time and the observer’s measurement scale distort the apparent accounting of energy, producing illusions of gain or depletion.
Black holes serve as relay nodes, not annihilators: they absorb, store, and re-emit energy through gravitational work, relativistic jets, or Hawking processes, effectively changing the address of energy rather than eliminating it. Thus, what seems like energy “death” in one domain reappears as energy “birth” in another, unified through an underlying conservation network embedded in the fabric of curved space-time.
The apparent “new” energy observed at cosmic scales—whether in accelerated expansion, radiation backgrounds, or jet emissions—is not an act of creation, but a consequence of scale remapping. As the universe evolves geometrically, the same conserved energy is continuously re-labeled and re-channeled, preserving the total ledger while shifting its manifestation across space, time, and scale.
Abstract
I proposed that energy is never destroyed, only transferred, with black holes acting as conduits and the universe itself as the medium. This concept suggests that every apparent disappearance of energy corresponds to its reappearance elsewhere—across scales, geometries, or states of matter.
We formalize this as a theorem about scale-linked conservation, where energy density obeys strict local continuity, yet its manifestations differ depending on the observer’s reference frame and scale of description. At the atomic scale, conservation appears through quantized exchanges; at the stellar and galactic scales, through gravitational dynamics and radiation; and at the cosmological scale, through curvature-induced redshift and metric expansion. What observers interpret as loss or creation of energy is often a translation error between these scales, not a violation of the conservation law.
Two key distortions drive these misinterpretations: (a) space-time curvature, which bends the flow of energy and modifies the perceived boundaries of a system’s energy ledger, and (b) coarse-graining or remapping, where complex micro-flows become invisible under macro descriptions, creating the illusion of “emergence” or “decay.” The universe, therefore, behaves as a multi-layered accounting network, constantly balancing local transactions through scale transformations and geometric reconfigurations.
To formalize this, we introduce a scale operator (
𝑆
𝑘
S
k
) that links energy distributions across hierarchical levels of structure, and a transfer graph with black-hole nodes representing energy relays. These relays do not destroy energy—they temporarily store and re-route it, emitting through jets, radiation, or Hawking channels. Under a set of mild axioms, the theorem demonstrates that the total energy within any closed region, when properly corrected for its scale-map boundary, equals the sum of fluxes entering and exiting through physical or scale-based relays.
From this foundation, we derive testable corollaries connecting horizon thermodynamics, gravitational time dilation, and multi-scale energy continuity. These implications reveal that so-called “energy disappearance” events—such as matter absorption by black holes or redshift losses in an expanding universe—are part of a broader relay network of persistence, where energy perpetually changes form and address, but never ceases to exist.
Definitions
Local Energy Density (
𝜌
(
𝑥
,
𝑡
)
ρ(x,t))
Effective energy per unit volume in a chosen reference frame. It represents the localized concentration of energy—whether kinetic, thermal, gravitational, or electromagnetic—within a specific region of space-time.
This term anchors the conservation law at the smallest resolvable level. Variations in
𝜌
ρ reflect how energy is distributed or redistributed due to curvature, compression, or expansion within that localized frame. It acts as the fundamental “entry” in the universe’s energy ledger.
Flux (
𝐽
(
𝑥
,
𝑡
)
J(x,t))
Energy flow vector field describing the rate and direction of energy transfer through space.
Flux quantifies the movement of energy between regions, analogous to current in electromagnetism or mass flow in fluid dynamics. It accounts for how energy propagates, radiates, or is absorbed through physical or geometric boundaries, and thus defines the “motion” of conservation itself.
Scale Map (
𝑆
𝑘
S
k
)
A reversible coarse-/fine-graining transformation that moves descriptions between adjacent scales
𝑘
↔
𝑘
+
1
k↔k+1 (atomic → molecular → stellar → galactic → cosmic).
This operator redefines how energy is described rather than how it behaves. When an observer shifts scale—zooming in or out—the apparent energy values change due to aggregation, averaging, or emergent phenomena. The scale map ensures that despite these apparent changes, the total underlying energy remains consistent when properly renormalized.
Relay Node (
𝑅
R)
A space-time structure that can absorb, transform, and later emit energy in altered form, location, or scale (e.g., event horizon, Rindler horizon, de Sitter horizon).
Relays act as energy intermediaries, capturing flows that momentarily disappear from observation and releasing them under different geometric or temporal contexts. They bridge discontinuities in perception—where energy seems to vanish—by maintaining continuity within a broader framework of hidden transfer.
Black-Hole Relay (
𝑅
B
H
R
BH
)
A specialized relay possessing an event horizon with characteristic surface gravity (
𝜅
κ) and area (
𝐴
A).
Unlike a sink, a black-hole relay functions as a gravitational router, storing energy in curvature and releasing it through jets, Hawking radiation, or other emission channels. Its surface parameters (
𝜅
,
𝐴
κ,A) determine its exchange rate, linking thermodynamics and geometry into one coherent conservation mechanism.
Scale Boundary (
∂
𝑆
𝑉
∂
S
V)
The interface where transitions in description scale transfer energy between different accounting ledgers—what exits one level of analysis enters another.
This boundary ensures continuity across perception: an energy flux that disappears at one resolution reappears at another. It represents the “translation layer” of the universe’s conservation law, preserving total energy through continuous exchange between scales, perspectives, and geometric domains.
Axioms / Premises
Lemmas
L1 (Hidden Flow Lemma).
If a flux line terminates on a relay, its continuation may re-emerge elsewhere or at a different scale through
Φ
𝑅
→
⋅
Φ
R→⋅
; thus, disappearance at one ledger implies appearance in another.
This lemma establishes the principle that energy flow is never truly discontinuous—only redirected. When an energy current encounters a relay, such as a black hole or horizon, the apparent termination of that current represents a change in visibility, not annihilation. The hidden portion of the flux continues beyond the observer’s geometric or temporal reach, resurfacing later as an emission, outflow, or re-scaled phenomenon.
Mathematically, the divergence of
𝐽
J is locally zero, but the domain of observation may exclude hidden channels through which the flux persists. Conceptually, this lemma explains why cosmic jets, background radiation, or delayed emissions appear in systems where energy seems to have vanished—they are re-expressions of hidden flow continuity.
L2 (Scale Ledger Lemma).
If the scale operator
𝑆
𝑘
S
k
changes, apparent sources or sinks can arise from
𝑍
𝑘
Z
k
-reweighting even under strict local continuity.
This lemma shows that when the scale of description shifts—such as moving from microscopic to macroscopic representations—the perceived amount of energy can fluctuate, not because of real creation or destruction, but because of the renormalization factor
𝑍
𝑘
Z
k
applied to preserve total consistency.
Energy observed at one scale might appear larger, smaller, or transformed at another due to the differing “resolution” of measurement. Coarse-graining hides microstructures that store energy, while fine-graining reveals energy previously unaccounted for. Hence, the conservation law must be expressed in scale-adjusted terms, ensuring that every ledger, regardless of scale, balances once the reweighting is applied.
L3 (Horizon Masking Lemma).
For observers outside a black-hole relay
𝑅
B
H
R
BH
, part of the flux
𝐽
J is geometrically masked; balance is restored by including horizon terms.
This lemma addresses the observer-dependent visibility of energy near extreme gravitational curvature. The event horizon acts as a geometric filter, concealing portions of flux from external measurement while maintaining the internal-external energy balance.
From an outside perspective, energy appears to vanish as it crosses the horizon. However, once horizon thermodynamics is considered—via surface gravity, area, and Hawking processes—the missing terms reappear as measurable emissions or curvature work. Thus, conservation remains intact, but the full balance requires horizon-inclusive accounting, where geometry itself becomes an active term in the energy equation.
Theorem (Scale-Linked Persistence)
Corollaries
Relay, Not Graveyard.
Black holes, though they represent the universe’s most extreme energy traps, are not final destinations. They maximize capture cross-section, pulling in matter and radiation with overwhelming gravitational force, yet the total energy balance remains closed.
Through relativistic jets, Hawking radiation, and frame-dragging emissions, black holes act as relay mechanisms that eventually redistribute what they absorb. Energy stored in the curvature of space-time around the horizon is later released—sometimes over cosmic timescales—ensuring that no energy is ever lost, only delayed and transformed. Thus, every black hole is a temporary relay station, not a graveyard of physics.
Scale Mirage.
What appears to be “energy creation” or “decay” in an expanding or contracting background often arises from scale misinterpretation. The changing values of the renormalization factor
𝑍
𝑘
Z
k
and the shifting boundaries of the scale map
∂
𝑆
𝑉
∂
S
V alter how energy is recorded across levels of observation.
When the universe expands, observers at a given scale perceive redshifted light and diluted density, giving the illusion that energy has been lost. However, once scale factors and geometric work terms are included, the balance restores perfectly. The mirage disappears when energy is evaluated through the complete multi-scale ledger, revealing that nothing has been created or destroyed—only re-labeled under a changing metric.
Time-Dilation Accounting.
In strong gravitational fields, time itself becomes an uneven variable of measurement. Near massive bodies, clocks slow, and fluxes appear to weaken or stall from an external viewpoint.
This corollary demonstrates that when redshift and time dilation corrections are properly included, the apparent energy imbalance vanishes. What looked like missing power or fading intensity is, in reality, energy stretched through time. The slower local clock does not lose energy—it redistributes it across a longer temporal frame, preserving total conservation once both reference frames are unified.
No Free Birth.
The notion of the universe “feeding” itself with newly created energy is an observational illusion born of geometric evolution. As curvature shifts and cosmic expansion modifies the scale structure, previously masked energy becomes visible in new domains—radiation fields, matter conversions, or dark-energy effects.
Thus, the universe’s apparent self-generation is actually continuous re-addressing of existing energy through evolving geometry. No new energy is born ex nihilo; rather, the total reservoir constantly changes its expression, maintaining eternal conservation while giving rise to the dynamic appearance of growth, decay, and rebirth across cosmic epochs.
Predictions / Falsifiability Hints
P1 (Horizon Ledger Closure).
For accreting black holes, the complete energy budget—composed of inflow power, change in black hole mass-energy, and emitted power through jets and radiation—should sum to approximately zero once relativistic redshift and geometric effects are properly accounted for.
This prediction implies that no hidden energy sinks exist inside the event horizon when viewed through the full relay accounting model. Energy entering the system either remains as stored curvature mass-energy or reappears through measurable outflows. Empirical validation can be sought in X-ray binaries, active galactic nuclei (AGN), and quasars, where simultaneous monitoring of accretion inflows, radiative emissions, and relativistic jet power can test the closure of the horizon ledger.
P2 (Scale Drift Signal).
In cosmological models that use coarse-graining or large-scale averaging, the so-called “missing” energy—often attributed to dark energy or unexplained redshift losses—should diminish when recalculated using explicit renormalization factors
𝑍
𝑘
Z
k
and including horizon-related contributions.
This prediction suggests that part of the universe’s energy imbalance originates from scale distortion, not new physics. When corrected for scale drift, the total energy density across cosmic epochs should converge more tightly to a constant. Observational cosmology can test this through re-analysis of CMB energy density, supernova redshift data, and gravitational lensing energy transfer, comparing uncorrected and scale-adjusted models.
P3 (Jet-Relay Coupling).
The evolution of a black hole’s spin and event horizon area should correlate directly with the energy output observed in its relativistic jets, consistent with the black hole acting as an energy relay node.
This prediction links angular momentum extraction and magnetohydrodynamic processes to the relay principle: as energy flows into the black hole, a proportional outflow manifests in jets, balancing the ledger through curvature work. Long-term radio and X-ray observations of AGN jet dynamics and spin-down rates should reveal this coupling quantitatively, confirming that the energy relayed through jets equals the curvature energy lost by the rotating horizon.
P4 (Hawking Channel Balance).
In systems where Hawking-like channels are experimentally accessible—such as acoustic black holes, optical event horizons, or Bose–Einstein condensate analogues—total energy conservation should hold once the scale flux term is explicitly included.
This prediction asserts that radiation emitted through quantum horizon analogues is not spontaneous creation but the re-expression of hidden energy flux across the scale boundary. Laboratory analogues can test this by measuring the input and output power around artificial horizons; inclusion of the “scale flux” correction should yield a balanced energy ledger. Such verification would bridge quantum thermodynamics, relativity, and multi-scale conservation, supporting the theorem’s universality across both astrophysical and laboratory domains.
Objections & Replies
O1: GR says global energy isn’t strictly conserved in generic expanding universes.
R: The theorem is local plus scale-aware, not globally absolute in the Noether sense. General Relativity allows global non-conservation because the universe lacks a fixed time-translation symmetry; however, within any local region—when the proper scale and curvature terms are included—energy balance remains exact.
The theorem focuses on scale-linked continuity, showing that what appears as global loss or creation is a translation error between geometric frames or scale ledgers. Expanding space changes the effective “bookkeeping surface” through which energy is measured, giving the illusion of net change. When corrected for the scale factor, curvature work, and horizon terms, total conservation re-emerges. The universe does not lose energy—it redistributes it through its evolving metric.
O2: “Energy reappearing elsewhere” sounds mystical.
R: It is not mystical—it is bookkeeping physics. Every inflow to a relay equals the sum of stored curvature energy and outgoing channels such as radiation, jets, or wave propagation.
The apparent “reappearance” results from hidden continuity across scales and horizons. When observers can only measure part of the flux—omitting regions masked by geometry or scale—they misinterpret balance as loss or spontaneous creation. Once all channels are included, including those hidden by horizons or coarse-graining, the total ledger closes precisely. The “reappearance” is therefore not metaphysical but a delayed or transformed manifestation of conservation.
O3: What about pure information loss?
R: The theorem addresses energy accounting, not the full scope of unitary information preservation. Energy conservation is a lower-order requirement independent of whether quantum information is fully retained.
If unitarity holds, then the relay mechanism preserves both energy and information, functioning as a perfect energy-information router. If unitarity is violated in extreme gravitational regimes, the theorem still stands at the energy level, ensuring that every measurable flow remains balanced even if microscopic informational patterns degrade. Thus, the theorem is agnostic to unitarity: it guarantees conservation of energetic continuity across geometry and scale, while leaving information flow to higher-order quantum interpretation.
Implications
Black-Hole Physics
Black holes should no longer be modeled as terminal sinks of energy but as gravitational routers within the universal energy network. Each black hole possesses a measurable inlet/outlet budget defined by accretion inflow, jet emission, radiative outflows, and Hawking processes.
By treating the event horizon as an active relay interface, physicists can quantify how much energy is stored in curvature versus how much is redistributed into the surrounding environment. This approach unifies black-hole thermodynamics with relativistic jet dynamics and horizon radiation, creating a closed-loop energy model where every inflow and outflow term can, in principle, be measured and balanced. Such a model transforms black holes from abstract singularities into empirically testable transfer systems within the broader conservation framework of the universe.
Multi-Scale Modeling
All physical models that span multiple observational or computational scales must explicitly publish their scale factors (
𝑍
𝑘
Z
k
) and scale-boundary assumptions (
∂
𝑆
𝑉
∂
S
V) to avoid misinterpretations of “energy creation” or “loss.”
When these factors are omitted, coarse-grained or over-simplified models can introduce phantom energy terms, leading to apparent violations of conservation that are purely mathematical artifacts. Including explicit renormalization coefficients and transition boundaries ensures scale continuity—that the total energy accounted for at one resolution reappears accurately in another. This practice becomes essential in computational astrophysics, cosmological simulations, and even condensed-matter systems where cross-scale coupling is significant.
Cosmology
In cosmological energy accounting, expanding space must be recognized as an energetic participant, not a passive background. The geometry of the universe performs measurable work on energy fluxes, redistributing them across curvature and scale.
Therefore, when interpreting the universe’s energy budget—dark energy, cosmic microwave background, or redshift phenomena—one must include geometric work terms and horizon contributions explicitly. The apparent “loss” of photon energy due to redshift or the “creation” of vacuum energy through expansion can both be resolved through proper inclusion of these terms.
This reframes cosmology as a scale-aware conservation system, where total energy remains invariant once the correct geometric corrections are applied. In this view, the universe is a self-consistent energy relay, continuously balancing its own fluxes through curvature, horizons, and scale transitions rather than violating conservation laws.
Minimal Working Formulae
This relation expresses local continuity of energy density (
𝜌
ρ) and flux (
𝐽
J), modified by relay interactions. Each term
𝜎
𝑟
σ
r
represents the net energy exchanged with a relay node located at
𝑥
𝑟
x
r
: positive when energy flows into the relay, negative when it exits.
The delta function
𝛿
(
𝑥
−
𝑥
𝑟
)
δ(x−x
r
) confines the exchange to the spatial location of the relay, ensuring that energy balance holds across both ordinary regions and embedded curvature nodes. Physically, this formula unifies field-level continuity with horizon and boundary exchanges, giving a local snapshot of how the universe’s energy is continuously re-channeled through its relay network.
This formulation defines energy (
𝐸
𝑘
E
k
) at a given scale level
𝑘
k through the renormalization factor
𝑍
𝑘
Z
k
, maintaining consistency between micro- and macro-descriptions. The first surface integral accounts for physical flux across the region’s boundary, while the second incorporates scale-flux—energy crossing between scales due to coarse-graining or fine-graining transitions.
The summation of relay fluxes ensures that all black-hole, horizon, or curvature-mediated exchanges are properly included. When computed together, these terms guarantee full conservation across both space and scale, forming a closed multi-scale ledger of universal energy flow.
This thermal-proxy equation treats the black hole as a convertor of inflow to outflow. The term
Φ
⋅
→
B
H
Φ
⋅→BH
represents accretion inflow power; the right-hand components quantify energy re-emitted through jets, radiation, and Hawking channels.
When measured over sufficient timescales and corrected for relativistic redshift, this balance should converge to zero, verifying that black holes are energetic relays rather than sinks. They temporarily store curvature energy (
𝑀
˙
𝑐
2
M
˙
c
2
) and later redistribute it through diverse emission pathways, completing the conservation cycle predicted by the Scale-Linked Persistence Theorem.
Formal Summary (Publication Box)
Scale-Linked Persistence Theorem:
In a curved and dynamically evolving universe, local energy conservation remains inviolable when two key factors are explicitly included:
(i) the presence of horizon-like relays (such as black holes, Rindler, or cosmological horizons) that temporarily store and re-emit energy, and
(ii) the cross-scale remapping that occurs as physical systems are viewed under different descriptive resolutions—from atomic to cosmic.
Apparent phenomena of energy creation or disappearance are thus reinterpreted as transfers—not violations—occurring through the universe’s network of geometric and scale transitions.
Black holes emerge as relay nodes that re-address energy across time, geometry, and scale, ensuring that what is seemingly lost in one domain reappears in another. They are not true sinks but dynamic routers in the universal conservation framework, upholding the continuity of energy through transformation, curvature, and multi-scale translation.